7.12 Digital Bubble Level

A bubble Level, is an instrument designed to indicate whether a surface is horizontal (level) or vertical (plumb). There are different types of spirit levels used by carpenters, stonemasons, bricklayers, other building trades workers, surveyors, millwrights, and other metalworkers, as well as in some photographic and videographic work.

Here we make a digital bubble level using MPU6050 and 8x8 LED matrix. When you deflect the MPU6050, the bubble on the LED matrix will also be deflected.

Required Components

In this project, we need the following components.

It’s definitely convenient to buy a whole kit, here’s the link:

Name	ITEMS IN THIS KIT	LINK
Kepler Kit	450+	Kepler Kit

You can also buy them separately from the links below.

SN	COMPONENT	QUANTITY	LINK
1	Raspberry Pi Pico W	1	BUY
2	Micro USB Cable	1
3	Breadboard	1	BUY
4	Jumper Wires	Several	BUY
5	LED Dot Matrix	1
6	74HC595	2	BUY
7	MPU6050 Module	1

Schematic

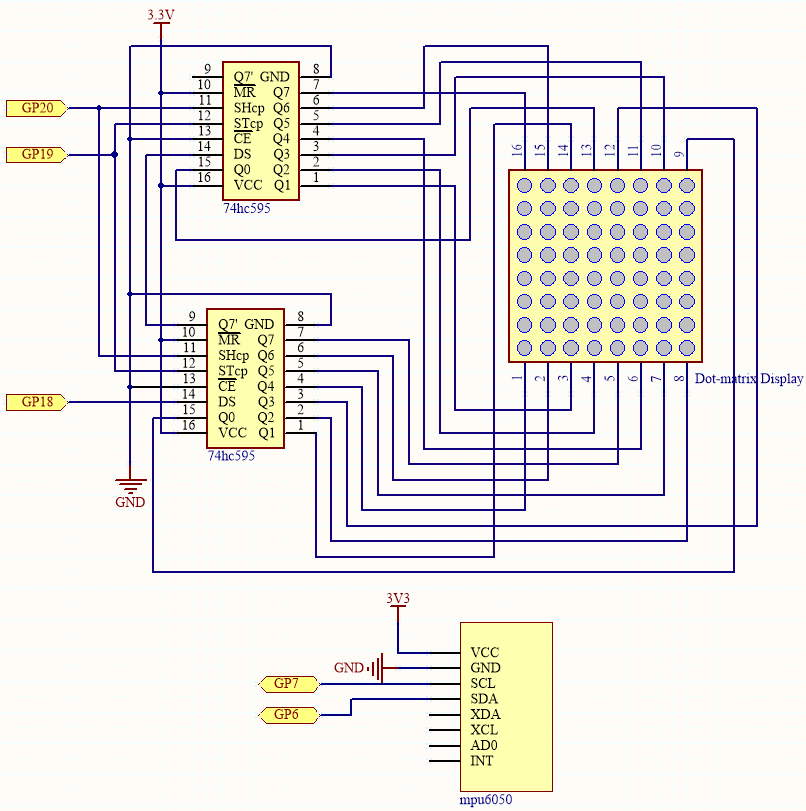
The MPU6050 takes the acceleration values in each direction and calculates the attitude angle.

As a result, the program draws a 2x2 dot on the dot matrix based on data from the two 74HC595 chips.

As the attitude angle changes, the program sends different data to the 74HC595 chips, and the position of the dot changes, creating a bubble effect.

Wiring

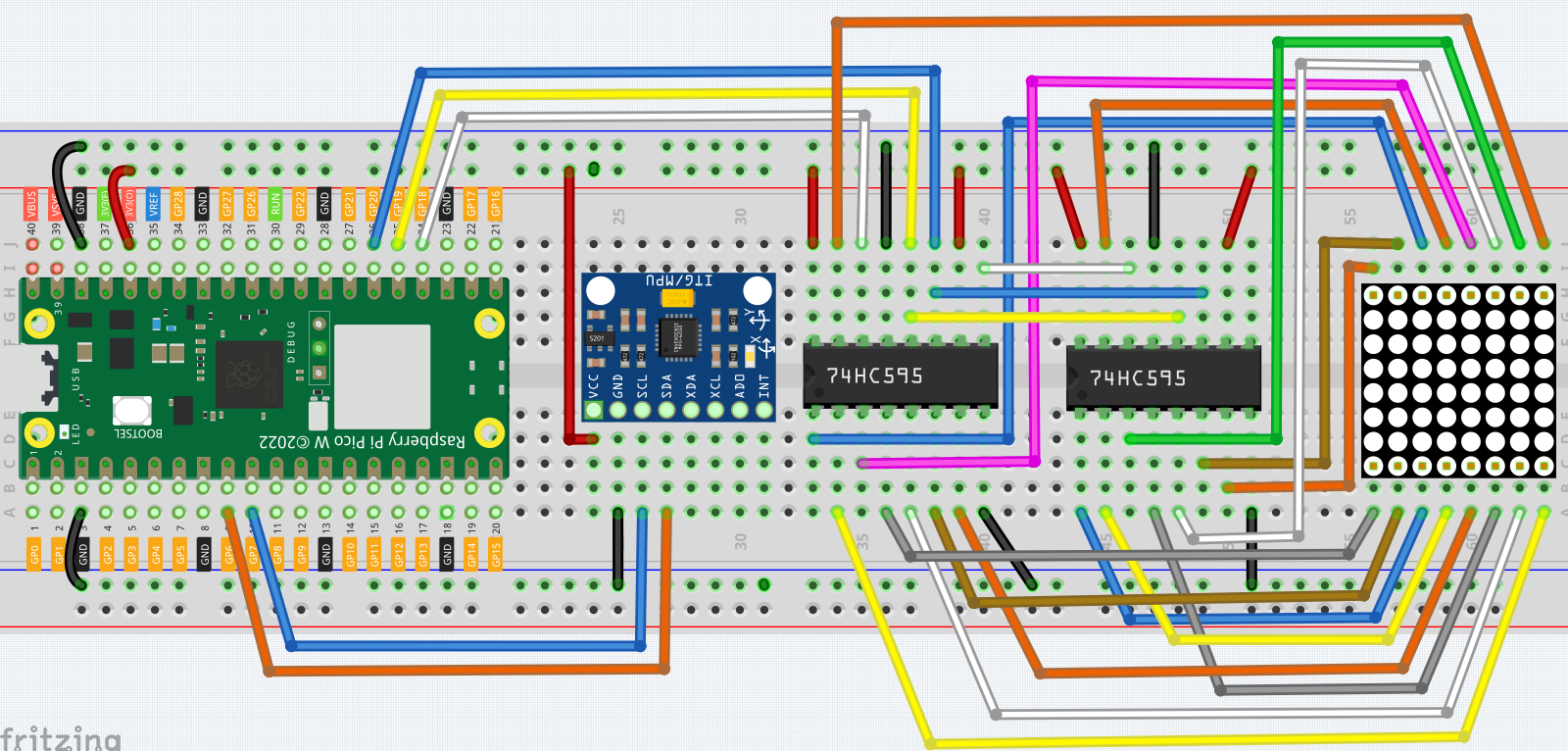
Code

Note

• Open the 7.12_digital_bubble_level.py file under the path of kepler-kit-main/micropython or copy this code into Thonny, then click “Run Current Script” or simply press F5 to run it.

• Don’t forget to click on the “MicroPython (Raspberry Pi Pico)” interpreter in the bottom right corner.

• For detailed tutorials, please refer to Open and Run Code Directly.

• Here you need to use the imu.py and vector3d.py, please check if it has been uploaded to Pico W, for a detailed tutorial refer to 1.4 Upload the Libraries to Pico.

import machine
from machine import I2C, Pin
import time
import math
from imu import MPU6050


### mpu6050
i2c = I2C(1, sda=Pin(6), scl=Pin(7), freq=400000)
mpu = MPU6050(i2c)

# get rotary angle
def dist(a,b):
    return math.sqrt((a*a)+(b*b))

def get_y_rotation(x,y,z):
    radians = math.atan2(x, dist(y,z))
    return -math.degrees(radians)

def get_x_rotation(x,y,z):
    radians = math.atan2(y, dist(x,z))
    return math.degrees(radians)

def get_angle():
    y_angle=get_y_rotation(mpu.accel.x, mpu.accel.y, mpu.accel.z)
    x_angle=get_x_rotation(mpu.accel.x, mpu.accel.y, mpu.accel.z)
    return x_angle,y_angle

### led matrix display
sdi = machine.Pin(18,machine.Pin.OUT)
rclk = machine.Pin(19,machine.Pin.OUT)
srclk = machine.Pin(20,machine.Pin.OUT)

def hc595_in(dat):
    for bit in range(7,-1, -1):
        srclk.low()
        time.sleep_us(30)
        sdi.value(1 & (dat >> bit))
        time.sleep_us(30)
        srclk.high()

def hc595_out():
    rclk.high()
    time.sleep_us(200)
    rclk.low()

def display(glyph):
    for i in range(0,8):
        hc595_in(glyph[i])
        hc595_in(0x80>>i)
        hc595_out()

# data transformation
def matrix_2_glyph(matrix):
    glyph= [0 for i in range(8)] # glyph code for display()
    for i in range(8):
        for j in range(8):
            glyph[i]+=matrix[i][j]<<j
    return glyph

def clamp_number(val, min, max):
    return min if val < min else max if val > max else val

def interval_mapping(x, in_min, in_max, out_min, out_max):
    return (x - in_min) * (out_max - out_min) / (in_max - in_min) + out_min

# Calculate the position of the bubble
sensitivity=4          # The higher the number, the more sensitive
matrix_range=7         # The size of the matrix is 8, so the coordinate range is 0~7
point_range=matrix_range-1     # The x, y value of the bubble's marker point (upper left point) should be between 0-6
def bubble_position():
    x,y=get_angle()
    x=int(clamp_number(interval_mapping(x,-90,90,0-sensitivity,point_range+sensitivity),0,point_range))
    y=int(clamp_number(interval_mapping(y,-90,90,point_range+sensitivity,0-sensitivity),0,point_range))
    return [x,y]

# Drop the bubble into empty matrix
def drop_bubble(matrix,bubble):
    matrix[bubble[0]][bubble[1]]=0
    matrix[bubble[0]+1][bubble[1]]=0
    matrix[bubble[0]][bubble[1]+1]=0
    matrix[bubble[0]+1][bubble[1]+1]=0
    return matrix

while True:
    matrix= [[1 for i in range(8)] for j in range(8)]  # empty matrix
    bubble=bubble_position() # bubble coordinate
    matrix=drop_bubble(matrix,bubble) # drop the bubble into empty matrix
    display(matrix_2_glyph(matrix)) # show matrix

Once you have run the program, place the breadboard on a level surface. A dot will appear in the center of the LED matrix (if it isn’t in the center, the MPU6050 may not be level). When you deflect the breadboard, the dot will move in the direction you deflected.